Hvordan finder jeg ligningen for en ret linje?

Linjens ligning

En ret linje har altid formen:

\(y = ax + b\)

Det kaldes også for en førstegradsligning.

\(a\) er hældningskoefficienten, og fortæller hvor meget linjen skråner.

\(b\) er det punkt på y-aksen (den lodrette akse), hvor linjen skærer.

1. Hvis linjen allerede er indtegnet i et koordinatsystem

Lad os starte med at kigge på en linje, som er indtegnet i et koordinatsystem:

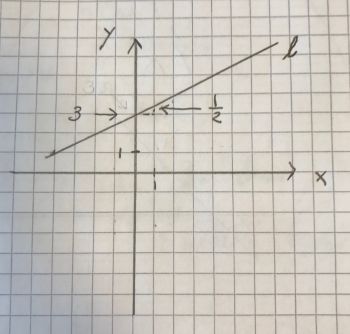
\(a\) (hældningskoefficienten) finder vi ved at tælle, hvor meget linjen l hælder, når vi bevæger os ét felt mod højre i koordinatsystemet. På illustrationen ovenfor hælder den med ½ tern.

\(b\) finder vi ved at aflæse, hvor linjen l skærer med y-aksen. På illustrationen skærer den ved \(3\).

Linjens ligning bliver dermed:

\(y = ½x + 3\)

Her er en linje mere indtegnet i et koordinatsystem:

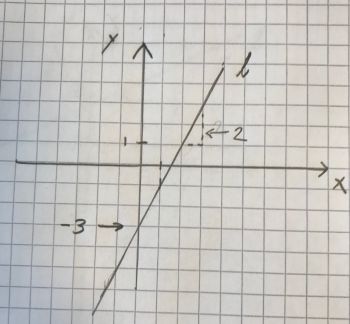
Hældningskoefficienten, \(a\), er her på \(2\).

\(b\), skæring med y-aksen, er \(-3\).

Vi får derfor ligningen:

\(y = 2x -3\)

2. Hvis vi kun kender ét punkt på linjen og dens hældning

Når vi kun kender et vilkårligt punkt på en ret linje sammen med hældningen, kan vi finde linjens ligning ud fra formen:

\(y - y0 = a * (x - x0)\)

\(y - y0 = a(x - x0)\)

Til eksempel kan vi tage en ret linje med punktet \((x,y)\) = \((3,5)\), og en hældning på \(2\).

Vi indsætter de værdier, vi kender:

\(y - 5 = 2(x - 3)\)

Vi isolerer \(y\):

\(y = 2(x - 3) + 5\)

Parentesen hæves:

\(y = 2x - 6 + 5\)

Det giver:

\(y = 2x - 1\)

3. Hvis vi kun kender to koordinater på linjen

Vi kan også have en situation, hvor vi kun kender to punkter på en linje, og bliver bedt om at bestemme ligningen.

Her gælder det, at vi finder hældningskoefficienten \(a\), ved :

\(a = \dfrac{y2 - y1}{x2 - x1}\)

og \(b\), som er skæringen med y-aksen, finder vi med:

\(b = y1 - a * x1\)

Lad os tage et eksempel:

Find ligningen for den rette linje, som går igennem punkter \((x1, y1)\) = \((2,3)\) og \((x2, y2)\) = \((4,7)\)

\(a\) findes:

\(a = \dfrac{y2 - y1}{x2 - x1} = \dfrac{7 - 3}{4 - 2} = \dfrac{4}{2} = 2\)

og \(b\), som kan udregnes, nu hvor vi kender \(a\):

\(b = y1 - a * x1 = 3 - 2 * 2 = 3 - 4 = -1\)

Ligningen bliver derfor:

\(y = 2x - 1\)