Her er definitionen på en mængde

En samling af enkeltstående elementer danner en mængde. Tag for eksempel numrene 5, 10 og 15, som i sig selv er tre enkeltstående tal. Tilsammen danner de tre tal en mængde, der kan skrives som {5, 10, 15}.

Der findes mange forskellige typer af mængder. Her er nogen af dem, som ofte bruges:

  • Foreningsmængden
  • Fællesmængden
  • Delmængden
  • Komplementærmængden
  • Den tomme mængde

Nedenfor kigger vi på hver af de 5 typer.

Foreningsmængden

Hvis vi har to mængder, \(A\) og \(B\), så kan vi lægge dem sammen. Det skriver vi på denne måde:

\(A \cup B\)

Dermed har vi forenet de to mængder.

Eksempel: Lad os antage, at mængden \(A\) består af tallene {2, 4, 6} og \(B\) af tallene {6, 8, 10}. Foreningsmængden af de to er dermed tallene 2, 4, 6, 8, 10:

\(A \cup B = \) {2, 4, 6} \( \cup \) {6, 8, 10} \(=\) {2, 4, 6, 8, 10}

Læg mærke til at selv om tallet 6 optræder i både \(A\) og \(B\), så er det kun med én gang i foreningsmængden.

Vi kan også illustrere en foreningsmængde på denne måde:

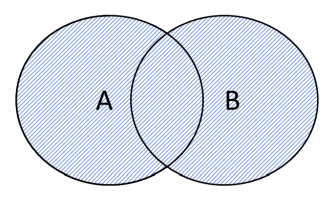
Foreningsmængden illustreret med cirklerne A og B

Foreningsmængden er alt det skraverede.

Det skal nævnes, at mængder ikke kun kan bestå af tal. Mængdeelementer kan være alt muligt: farver, mennesker, dyr - ja hvad som helst, der kan grupperes.

Fællesmængden

Fællesmængden består af de elementer fra mængderne \(A\) og \(B\) som er ens. Vi kan skrive det sådan:

\(A \cap B\)

Eksempel: Hvis mængden \(A\) indeholder tallene {1, 2, 3} og \(B\) tallene {2, 3, 4, 5}, så er fællesmængden tallene 2 og 3:

\(A \cap B = \) {1, 2, 3} \(\cap \) {2, 3, 4, 5} \(=\) {2, 3}

Fællesmængden kan illustreres sådan:

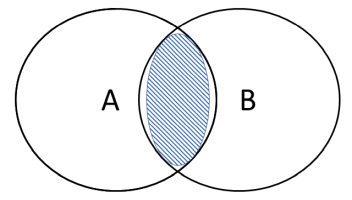
Fællesmængden er der hvor elementerne er ens for A og B

Det skraverede område markerer fællesmængden.

Delmængde

Når alle elementer af mængden \(A\) er indeholdt i \(B\), så er \(A\) en delmængde af \(B\). Det kan skrives sådan:

\(A \subseteq B\)

Eksempel: Lad os sige at \(A\) er en delmængde af \(B\). \(A\) består af tallene {2, 3} og \(B\) af tallene {1, 2, 3}. Delmængden bliver dermed tallene 2 og 3:

\(A \subseteq B = \) {2, 3} \( \subseteq \) {1, 2, 3} \(=\) {2, 3}

Med andre ord er resultatet \(A\).

Delmængden kan illustreres således:

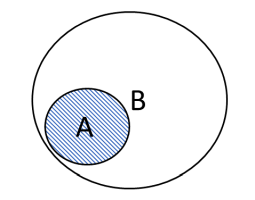
A er en delmængde af B

Det skraverede område markerer delmængden.

Komplementærmængden

Mængden af elementer i \(A\) som ikke er indeholdt i \(B\), kalder vi for komplementærmængden. Det skrives på denne måde:

\(A \setminus B\)

Eksempel: Hvis mængden \(A\) består af tallene {1, 2, 3} og \(B\) af tallene {2, 3, 4} så er komplementærmængden tallet 1:

\(A \setminus B = \) {1, 2, 3} \(\setminus \) {2, 3, 4} \( = \) {1}

Man kan også se det som, at \(A\) "trækkes fra" \(B\).

Komplementærmængden kan illustreres som vist her:

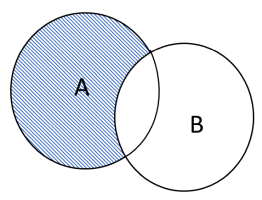
Komplementærmængden hvor A trækkes fra B

Den tomme mængde

Der findes også en tom mængde. Som navnet antyder, består den tomme mængde ikke af nogen elementer.

En tom mængde skriver vi med bogstavet Ø:

\( \emptyset \) eller {}

Øvelser

Øvelse 1: Find det rigtige svar

Hvad er foreningsmængden af mængderne A og B?

Det lidt nørdede

Der er intet til hinder for, at der indgår mere end to mængder. Her har vi eksempelvis tre mængder:

\(A \cap B \cap C\)

Det er blot nemmere at forklare mængdelære, når der kun indgår to mængder.

Rækkefølgen på elementerne i en mængde er ikke vigtig.

{1, 2, 3} = {3, 2, 1}

Hvis en mængde kun har ét element, kalder vi det for en singleton:

{3}

Beskrivelsen af en mængde med tuborgparenteser {1, 5, 7, 10} kaldes for Roster-notation.

Den tyske matematiker Georg Cantor opfandt i slutningen af 1800-tallet teorien omkring mængdelære. Han er også ophavsmand til Cantors diagonalbevis, der handler om ikke-tællelige mængder.

Relaterede artikler

Kommentarer

Siden her er senest opdateret: 29 Sep 2019 - relevante nøgleord: mængdelære, forening, statistik
Siden her er senest opdateret: 29 Sep 2019 - relevante nøgleord: mængdelære, forening, statistik