Hvordan finder jeg sidelængden i en vilkårlig trekant?

Sinusrelationerne

Lad os starte med at se på formlerne til sinusrelationerne for en vilkårlig trekant:

\(\cfrac{sin(A)}{a} = \cfrac{sin(B)}{b} = \cfrac{sin(C)}{c}\)

eller

\(\cfrac{a}{sin(A)} = \cfrac{b}{sin(B)} = \cfrac{c}{sin(C)}\)

hvor \(A\), \(B\), \(C\) er hjørnernes vinkler og \(a\), \(b\), \(c\) er sider.

Tag et kig på trekanten nedenfor, hvor vi kender de to hjørnevinkler \(A\) og \(C\) og siden \(a\).

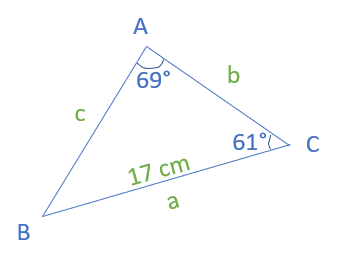
Lad os tage et eksempel så vi kan afprøve sinusrelationerne:

Beregn sidelængderne på \(b\) og \(c\) for trekanten på billedet.

Vi kender, som tidligere nævnt, hjørnevinklerne \(A\) og \(C\), som er henholdsvis 69 grader og 61 grader. Desuden kender vi længden på siden \(a\), som er 17 cm. Dermed har vi de tre oplysninger, der er nødvendige, for at kunne beregne sidelængderne \(b\) og \(c\) med sinusrelationerne.

Når du skal vælge mellem formlerne ovenfor, er det nemmeste at bruge den af dem, hvor den ubekendte du søger, står i tælleren (altså over brøkstregen).

Først kaster vi os over at finde længden på siden \(b\).

Vi finder formlen med den ubekendte i tælleren, som vi ønsker at finde (\(b\)). Den skal sættes lig en af de andre to formler, for at kunne beregnes; da vi kender både \(A\) (hjørnevinklen) og \(a\) (siden), vælger vi at sætte den lig med \(\cfrac{a}{sin(A)}\).

\(\cfrac{a}{sin(A)} = \cfrac{b}{sin(B)}\)

Men nu har vi to ubekendte: \(B\) og \(b\). Heldigvis kan vi beregne \(B\), da vi ved at vinkelsummen i en trekant altid er 180 grader:

\(B = 180° - 69° - 61° = 50°\)

Formlen omskriver vi nu fra:

\(\cfrac{a}{sin(A)} = \cfrac{b}{sin(B)}\)

til

\(b = sin(B) * \cfrac{a}{sin(A)}\)

Lad os indsætte de tal vi kender:

\(b = sin(50) * \cfrac{17 \space cm}{sin(69)} = 0,7660 * \cfrac{17 \space cm}{0,9336} = ca. \space 13,94 \space cm\)

Så nu har vi sidelængden på \(b\).

Ligeledes kan vi finde \(c\):

\(\cfrac{a}{sin(A)} = \cfrac{c}{sin(C)}\)

Omskriver vi til:

\(c = sin(C) * \cfrac{a}{sin(A)} = 0,8746 * \cfrac{17 \space cm}{0,9336} = ca. \space 15,93 \space cm\)

Nogen gange kan sinusrelationerne ikke bruges til at beregne sidelængder i en vilkårlig trekant. Det gælder for eksempel, hvis vi i en trekant kun kender én af vinklerne. Her kan vi i stedet bruge cosinusrelationerne.

Cosinusrelationerne

Formlerne til cosinusrelationerne der bruges til beregning af sidelængderne i en vilkårlig trekant, ser sådan ud:

I) \(a^2 = b^2 + c^2 - 2bc * cos(A)\)

II) \(b^2 = a^2 + c^2 - 2ac * cos(B)\)

III) \(c^2 = a^2 + b^2 - 2ab * cos(C)\)

Lad os prøve det af med et lille eksempel:

Trekanten \(ABC\) har en vinkel \(A\) på 30°, siden \(b\) på 20 cm og siden \(c\) på 25 cm. Beregn sidelængden \(a\).

Vi kender hjørnevinklen \(A\), og siderne \(b\) og \(c\). Det er derfor den første af formlerne (I), vi anvender:

\(a^2 = b^2 + c^2 - 2bc * cos(A)\)

\(a^2 = 20^2 \space cm + 25^2 \space cm - 2 * 20 \space cm * 25 \space cm * cos(30) = 400 \space cm + 625 \space cm - 1000 \space cm * 0,8660 = 1025 \space cm - 866 \space cm = 159 \space cm\)

\(a = sqr(159) \space cm = 12,61 cm\)

Siden \(a\) er dermed ca. 12,61 cm.